Delta V : KÉZAKO ?
Nouvel article de la série des « Kézako »! Qu’est-ce que le Delta-V ? Comment peut-il vous aider à organiser vos balades inter-planétaires ?
Qu’est-ce que le Delta-V ?
Comme à notre habitude, commençons par un peu de théorie : le Delta-V est une mesure de changement de vitesse qui est exprimée en mètres par seconde (m/s). Le Delta-V qu’est capable de fournir une fusée correspond en quelque sorte à un nombre de « points de mouvement » qui seront consommés au fur et à mesure de l’utilisation des systèmes de propulsions.
A quoi cela peut-il me servir ?
Le Delta-V permet tout d’abord de savoir ce que vous pourrez accomplir avec votre fusée. Prenons par exemple une mise en orbite autour de Kerbin : cette opération nécessite environ 4500 m/s de Delta-V. Si votre fusée est seulement capable de délivrer 3000 m/s Delta-V, il vous sera alors impossible de vous mettre en orbite car vous manquerez de carburant ! L’intérêt du Delta-V est de pouvoir être calculé dès la conception de votre fusée.
Le Delta-V est également pratique pour effectuer des améliorations sur vos fusées. En effet, il vous permettra de comparer rapidement l’efficacité de différentes optimisations que vous souhaiteriez mettre en place. Vous serez quelquefois surpris du nombre Delta-V que vous pourrez gagner en enlevant une ou deux petits éléments inutiles de votre fusée !
Comment récupérer / calculer le Delta-V ?
Le Delta-V ne figure pas dans le jeu. Le plus simple pour le récupérer est d’installer un Addon tel que MechJeb (pour la v2.x, c’est ici) ou Kerbal Engineer Redux. Ce type d’Addon permet de connaitre le Delta-V total ou pour chaque étage de votre fusée. Pendant le vol, vous pourrez voir le Delta-V être consommé en temps réel.
Voici un exemple des données que vous pouvez récupérer avec MechJeb :
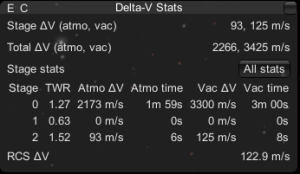
Statistiques Delta-V de MechJeb 2.0.x
De haut en bas :
- Stage Delta-V : indique le nombre de Delta-V pour l’étage en cours. Le chiffre de gauche correspond au Delta-V pour un déplacement dans l’atmosphère et celui de droit à un déplacement dans l’espace. En effet, la performance de certains systèmes de propulsion peut varier en fonction de la présence ou non d’atmosphère.
- Total Delta-V : idem que ci-dessus mais pour la totalité de la fusée.
- Stage stats : Détail du Delta-V pour chaque étage de la fusée avec une estimation du temps estimé de propulsion.
- RCS Delta-V : Qui n’est jamais tombé à court de carburant et a terminé sa mission au RCS ? Cette valeur vous donnera le Delta-V dont vous disposerez en cas de gros pépin !
Si vous êtes motivés, vous pouvez vous passer d’un Addon et calculer le Delta-V vous-même. Vous pouvez récupérer la formule magique sur cette page du Wiki officiel de KSP.
Delta-V nécessaire pour se déplacer dans le système solaire
Vous savez maintenant ce qu’est le Delta-V, à quoi il sert et comment le calculer. Voyons maintenant combien il vous en faudra pour vos balades inter-planétaires…
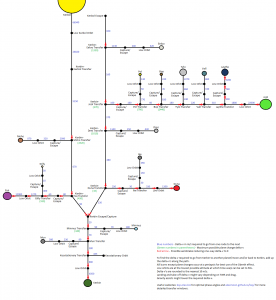
Voici un graphique assez précis que j’ai récupéré sur Internet. Il vous permettra de connaitre le Delta-V nécessaire pour vous balader dans le système solaire.
Traduction de la légende :
- Les nombres bleus indiquent le Delta-V en m/s nécessaire pour vous déplacer d’un nœud à l’autre.
- Les chiffres verts entre parenthèses indiquent le nombre de Delta-V maximum qui est nécessaire pour le changement d’inclinaison (lorsque l’astre ne se trouve pas sur le même plan).
- Les flèches rouges indiquent qu’il est possible de faire de l’aérofreinage pour réduire le nombre de delta-V nécessaire (dans le sens de la flèche uniquement bien entendu ^^)
Exemple
Prenons l’exemple d’un aller simple sur la Mun :
- Nous partons de Kerbin et allons nous mettre en orbite basse. Pour cela, il nous faut 4500 m/s de Delta-V.
- Nous allons ensuite faire grimper notre apogée jusqu’à se faire capturer par la Mun. Pour cela, il nous faut 680 Delta-V (apogée au niveau de l’orbite géostationnaire) + 180 + 80 (pour arriver jusqu’à la capture). La Mun se trouve sur le même plan que Kerbin, il n’y a donc pas besoin de modifier notre inclinaison.
- La mise en orbite autour de la Mun demandera 230 Delta-V supplémentaire.
- Et pour s’y poser il nous faudra encore 580 Delta-V.
Si on fait l’addition, on arrive à 6250 Delta-V. Il vous faudra donc concevoir une fusée d’au mois 6250 Delta-V pour espérer poser votre fusée sur la Mun.
3, 2, 1, à vos commentaires !







Je ne suis pas d’accord avec la définition du Delta-V. Ce n’est pas une quantité de mouvement mais une différence de vitesse (delta étant un symbole utilisé physique en pour qualifié une différence finie). En fait, il s’agit simplement de la différence de vitesse entre notre vitesse actuelle et la vitesse nécessaire pour une orbite-cible.
Merci pour ta remarque 😉 J’ai remplacé le terme « quantité de mouvement » qui n’était effectivement pas juste par « mesure de changement de vitesse ».
Le Delta en mathématique défini la différence. Je prend mon cas de motard: quand on dit qu’il ne faut pas remonter une file à plus de 30 km/h de Delta-V, cela veut dire que si les voitures avance à 20 km/h, il faut éviter de remonter la file à plus de 50 km/h.
Un bon début, qui mériterait un peu d’approfondissement sur les implications de ce paramètre que je contrôle personnellement très mal.
Un système disposant d’un pod, d’un réservoir long mince, et d’une propulsion Aerospike dispose-t-il d’autant de DV que le même ensemble à l’exception d’un nucléaire comme propulseur ?
Sauf erreur de ma part, le DV d’un système correspond à sa propension d’acquérir, dans un référentiel linéaire et isolé de toute force, une certaine vitesse, le DV en question. Cela s’équilibre d’ailleurs par conservation de la quantité de mouvement, un paramètre probablement plus parlant en ce qui me concerne.
Toujours est-il que nos situations de jeu ne sont pas coupées de toutes interactions extérieures. Au décollage, la fusée « pèse », et une partie de la puissance délivrée lutte contre la gravité plutôt que d’accumuler du DV.
En orbite, je me pose la question de l’inertie du système et du rôle de l’ISP. Un nucléaire, avec la même quantité de fuel, permettra sauf erreur d’acquérir un meilleur DV, car son « efficacité » (le terme n’est pas à prendre au sens énergétique du terme, c’est bancal) est supérieure, chaque litre promet plus d’impact. Toutefois, l’excédent de poids du nucléaire a-t-il une influence cette fois négative sur le potentiel du module ? L’inertie intervient… Beaucoup de paramètres qui s’emmêlent, mais j’imagine qu’aucun topo ne saurait les expliquer parfaitement en les dissociant. Il faudrait un véritable cours, qui serait illisible et prendrait un peu de temps à consigner proprement ^^
Enfin l’article reste une bonne introduction à qui se demande ce que peut bien vouloir dire ce terme qui ressort à toutes les sauces, merci 🙂
Je n’ai pas le jeu sous la main pour te donner le comparatif sur l’Aerospike et le moteur nucléaire. Mais je peux déjà te dire que le Delta-V sera plus élevé sur l’Aerospike dans l’atmosphère (le moteur nucléaire n’est pas performant du fait qu’il a une très faible ISP dans l’atmosphère). Je te laisse le soin de faire une comparaison avec MechJeb pour vérifier mes dires 😉
Pour calculer le Delta-V, on a besoin de connaitre la masse totale de la fusée, sa masse à vide (sans carburant) et l’ISP des moteurs. Le Delta-V tient donc compte de la masse du système de propulsion ainsi que de sa poussée et de sa consommation grâce à l’ISP.
Par ailleurs, le Delta-V indiqué dans le graphique prends en compte les pertes liées à la gravité (35% en moyenne) et au frottement avec l’air (20% en moyenne) pendant le décollage. Sans ces deux contraintes, il ne faudrait qu’un peu plus de 2000 Delta-V pour décoller de Kerbin 🙂
J’espère avoir éclairé ta lanterne…
Yup, c’était également ce que j’avais pu lire ci et là, j’avais eu le sentiment en lisant l’article que tu n’évoquais essentiellement que la quantité de carburant embarquée.
Par contre je ne savais pas que le graphique tenais globalement compte des pertes !
Merci du passage, je vais essayer de reprendre mes notes générales, y’a que comme ça je crois qu’on peut tenter de bien comprendre la mécanique mise en jeu, c’est difficilement dissociable :s
Je suis d’accord avec le commentaire du dessus. Je pense que c’est une certaine mesure, une indication pratique, mais pas à prendre au pied de la lettre.
Pour donner un exemple, j’ai fait une fusée qui permet d’aller sur la Mun. Celle-ci a moins de delta V total qu’il n’en ai prévu par le graphique pour s’y rendre. Donc il faut certainement aussi prendre en compte le chemin parcourue, les fenêtres et ce que l’on aime appeler « trajectoire économique ».
Mais sinon, très bon article, et surtout très instructif !! Merci
Le Delta-V indiqué dans le graphique est une moyenne. On peut effectivement en dépenser un peu moins, ou beaucoup plus 🙂
Je suis curieux, combien de Delta-V as tu économisé par rapport au graphique ?
Ha, j’ai dis des bêtises !
Si on calcul le Delta V pour aller sur la Mun, il en faut selon le graphique 6250.
Ma fusée (et c’est là que j’ai mal lu) a un Delta V de 5833 en atmosphère et 6780 dans le vide. La première fois que j’avais lu, je n’avais pas pris en compte la seconde mesure, du coup je pensais qu’il n’y en avais qu’un et que j’étais bien inférieur à ce qui était indiqué.
Tout s’explique 🙂
Excellent article qui m’a fait découvrir Mechleb que j’utiliserait pour le delta V par contre l’autopilote c’est un peu cheaté…
Je vais peut-être pourvoir sauver mes Kerbonautes bloqués sur Duna par manque de delta-V pour repartir.
Il y a un mod pas mal qui te permet d’avoir à peu près les mêmes informations que celles fournies par MechJeb: Kerbal Enginner Redux.
L’avantage c’est qu’il n’y a pas de pilotes automatiques ou autres, uniquement des valeurs concernant ton orbite ou ton vaisseau ^^.
Petit question. Dans le graphique, à quoi correspond une orbite basse ? Combien de m ?
Merci
Il n’y a rien de très précis pour définir une « orbite basse », mais pour te donner une idée :
– Astre avec atmosphère : environ 30 à 50 kms au dessus
– Autres astres : environ 50 kms de la surface.
et si on veut revenir de la mune ? il faut le meme DV pour le retour ?
Non, je ne pense pas. Les 4500 m/s de Kerbin, tu les as en rentrant dans l’atmosphère. Cependant, l’air de plus en plus dense en se rapprochant du sol vont te freiner et en quelque sorte de voler ce DV que tu acquiert. Mais comme tu vas être inlassablement attiré vers le sol. D’après le graphique il faut 580 pour se mettre en orbite autour de la Mun, 230 pour quitter l’influence de la Mun, 80 pour se transferer dans l’orbite de Kerbin, 180 pour atteindre l’orbite géostationnaire et 680 pour atteindre l’orbite bas de Kerbin, étant la limite de son atmosphère.
Mais j’ai du coup une question sur ce graphique. Ces delta V sont pour des mises en orbite parfaits (càd un cercle parfait, une apogée et périgée identique)? Si c’est le cas, en préparant bien la trajectoire de la fusée, il est possible d’aller le plus directement possible vers Kerbin (ou autre astre) sans passer par une orbite. Donc avoir recourt à moins de DV.
J’ai encore une autre question. C’est quoi les transferts? Comme Mun transfert, Eve transfert… Je vois pas trop ce que c’est…. Par exemple dans le cas de la Mun, on passe d’un orbite autour de Kerbin à l’orbite de la Mun directement, il n’y a pas de « transfert », dans mon cas